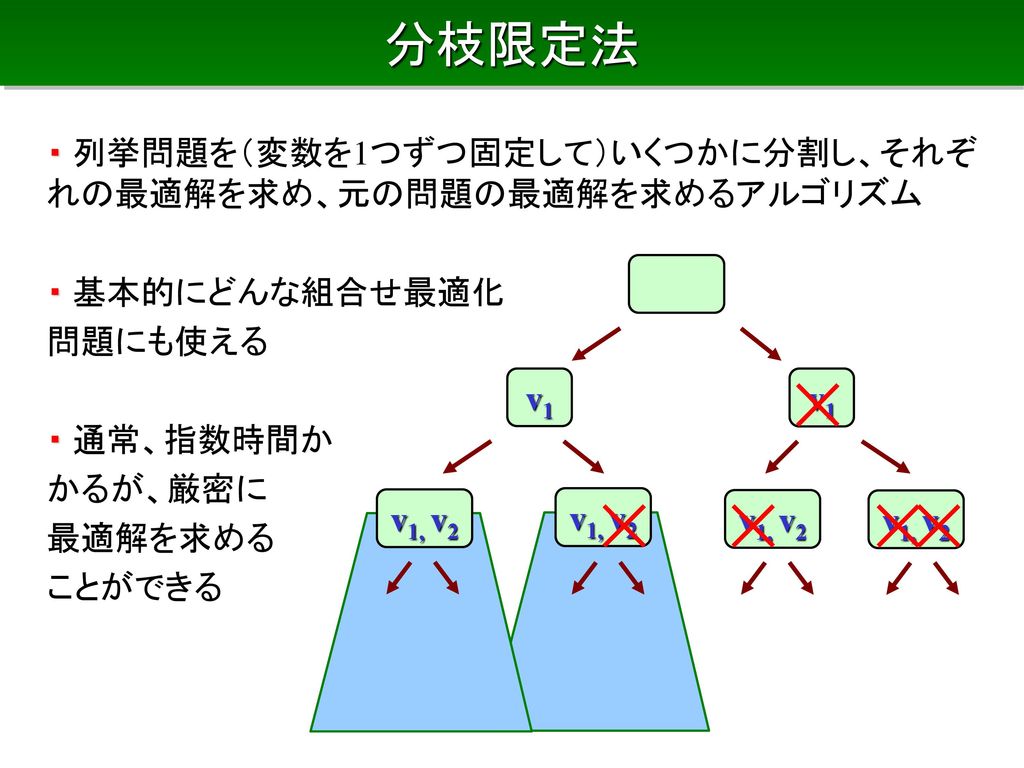
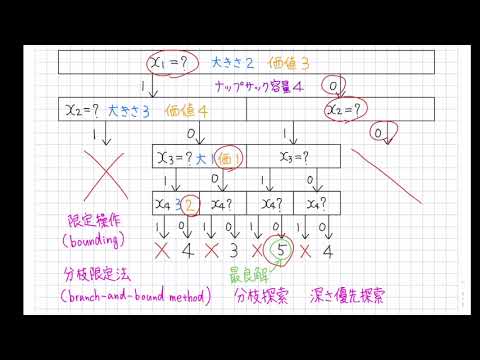
分枝限定法の考え方 •問題を場合分けによって部分問題に分解(分枝操作) •01ナップサック問題: 各変数について0 の場合と1 の場合に分ける •分枝の進行の様子は探索木により表現可能 •これだけでは解の全列挙と同じ,時間がかかる例ナップサック問題に対する分枝限定法 ナップサックの容量W max = 112 要素 重さ 6 25 30 40 30 60 10 腕づく 方 全数探索 合 検 す 解候補数 重さ 価値 15 100 90 60 40 15 10 3 ・腕づくの方法(全数探索)の場合、検討する解候補数は28=256分枝限定法 分枝カット法 動的計画法 ... 近似解法最適解を求めることを諦めて,ある程度最適値に近い値をもつ実 行可能解をなるべく早く求める 制度保証付き近似解法 メタヒューリスティック(タブーサーチ,遺伝的アルゴリズ ム,アニーリング法

Approximation Algorithms For Combinatorial Optimization Problems Speaker Deck
分枝限定法 ナップサック java
分枝限定法 ナップサック java-分枝限定法 ナップサック問題 最大化z = ∑n i=1 cixi 制約条件 ∑n i=1 aixi b xi 2f0;1g (i = 1;2;本記事は、ソフトバンクパブリッシングから発行されている「定本 Cプログラマのためのアルゴリズムとデータ構造 (SOFTBANK BOOKS)」を参考にPythonでアルゴリズムとデータ構造について学習していきます。 今回は、動的計画法によるナップザック問題(Knapsack Problem)について学んでいきます。



第2回 ナップサック問題を色々な方法で解いてみた ブレインパッドの数理最適化ブログ Platinum Data Blog By Brainpad
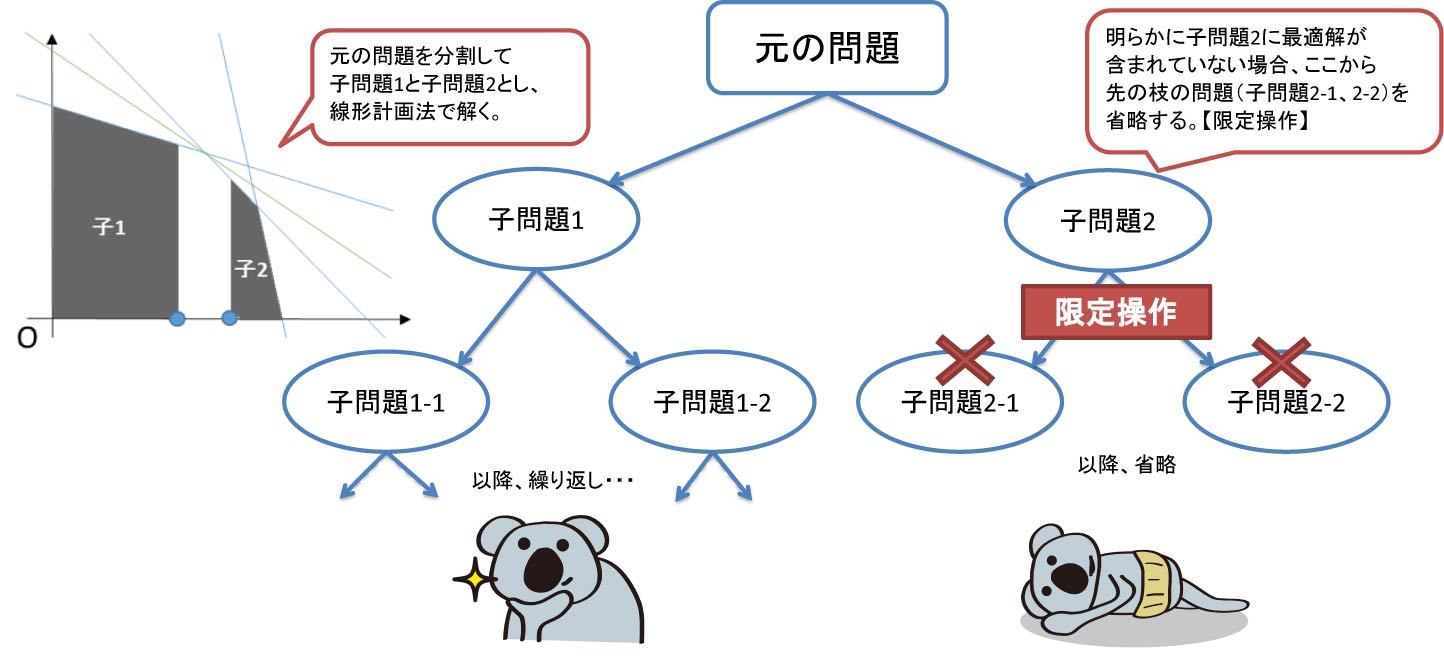
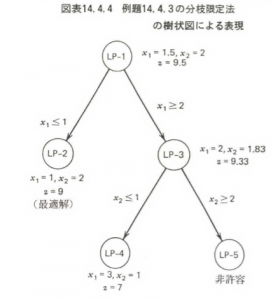
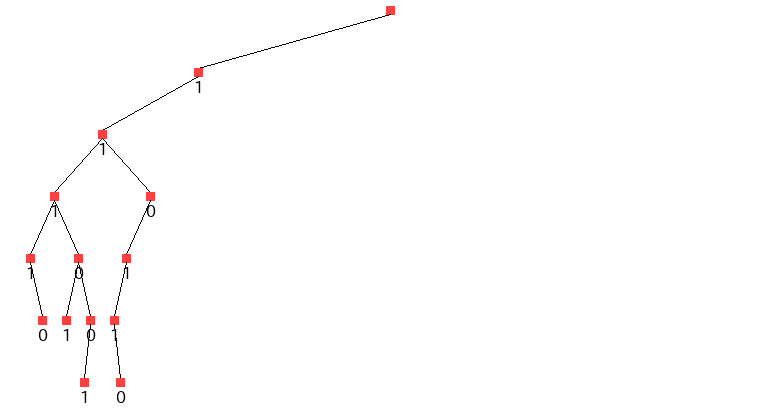
分枝操作: ∈0,1のいくつかを固定 緩和:連続化 ∈0,1により解の上界を与える –連続緩和した問題は簡単(𝑞 / が大きい方から詰めるだけ) 分枝限定法の別の例: ナップサック問題図1 01 ナップサック問題に対する分枝木 31 分枝限定法 分枝限定法は,一部の変数を固定しつつそれぞ れの場合を調べ上げていくという考え方に基づい ている.この過程は,図1 のような図(分枝木と 呼ぶ)を用いて表現できる.一番上の点1は元の分枝限定法の考え方 • 問題を場合分けによって部分問題に分解(分枝操作) • 01ナップサック問題: 各変数について0 の場合と1 の場合に分ける • 分枝の進行の様子は探索木により表現可能 • これだけでは,解の全列挙と同じ,時間がかかる
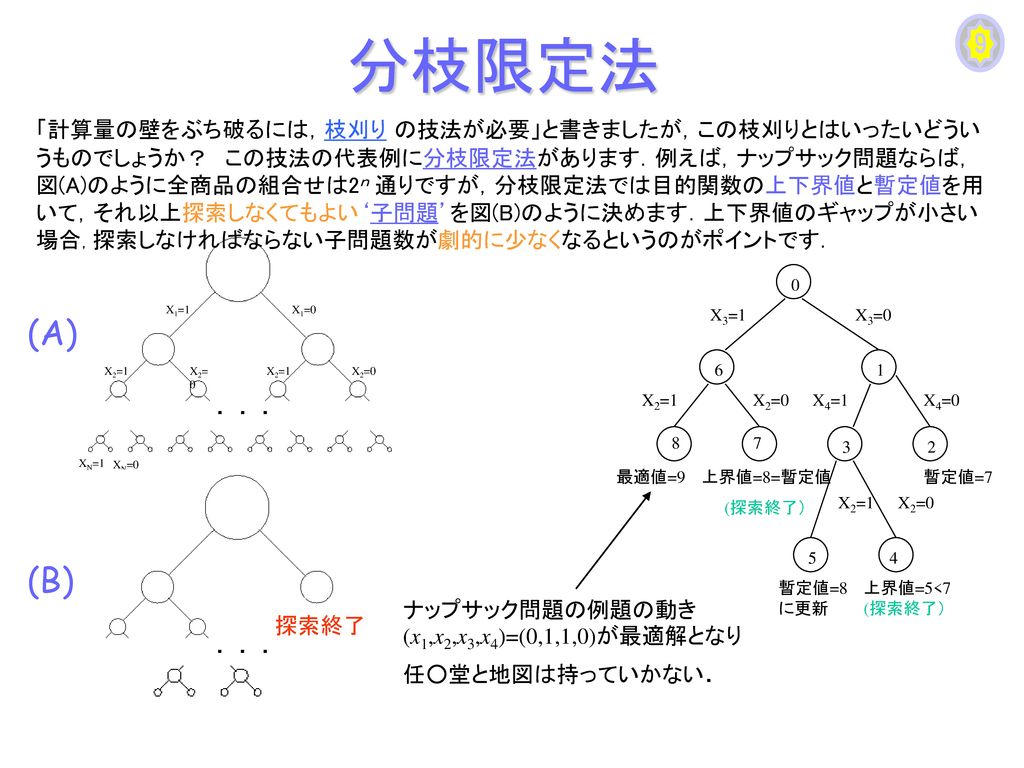
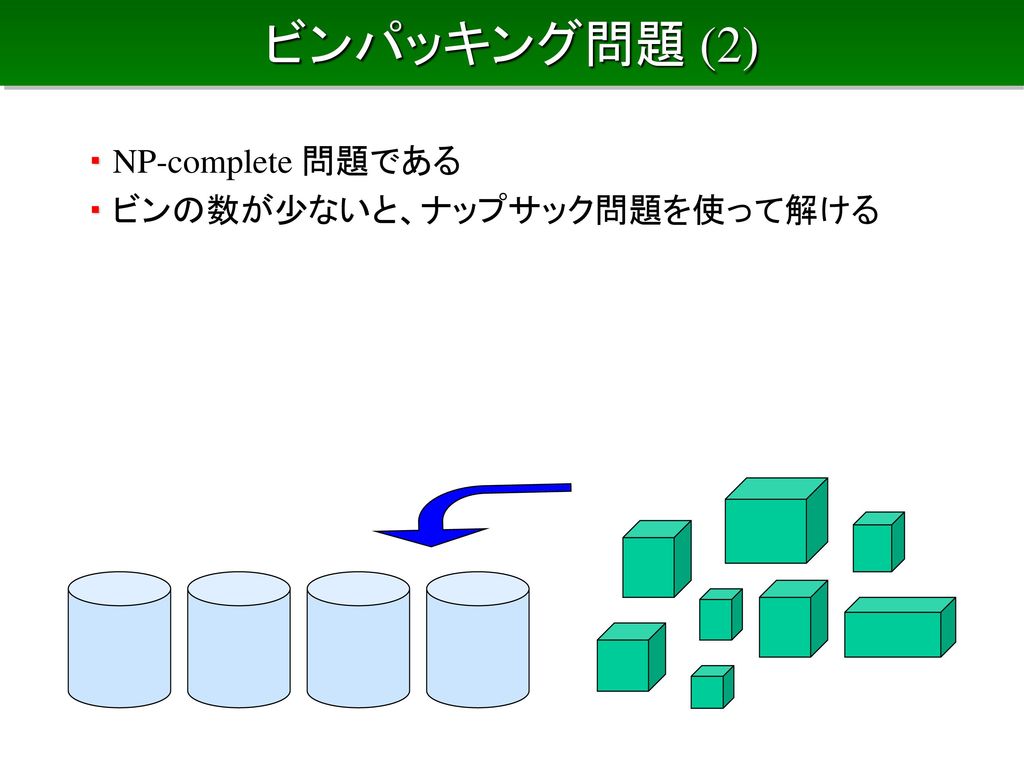
分枝限定法 帰着とnp完全性 分枝限定法 上界と下界による限定操作 ナップサック問題 ナップサック問題 (2) ビンパッキング問題 ビンパッキング問題 (2) 巡回セールスマン問題 問題の難度と解法 01整数計画として定式化 ハミルトンサイクルが解ける 問題の解法 分枝限定法(Branch and Bound) まず始めに01 ナップサック問題 を整数計画問題として定式化します. 変数 xi は値が 1 のとき i 番目のアイテムを選択し, 0 のとき選択をしないことに対応しています. 分枝限定法は変数の値を順番に0か1かに固定していき分枝木を探索していきます.探索の途中で変数 xi の値を決めるときに, x1, x2, , xi − 1 の値はは 0 または 1分枝限定法の考え方 • 組合せ計画問題を,場合分けによって部分問題に分解 (分枝操作) • 01ナップサック問題:各変数について0 の場合と1 の場合に分 ける • 巡回セールスマン問題:次に訪問する都市によって場合分け
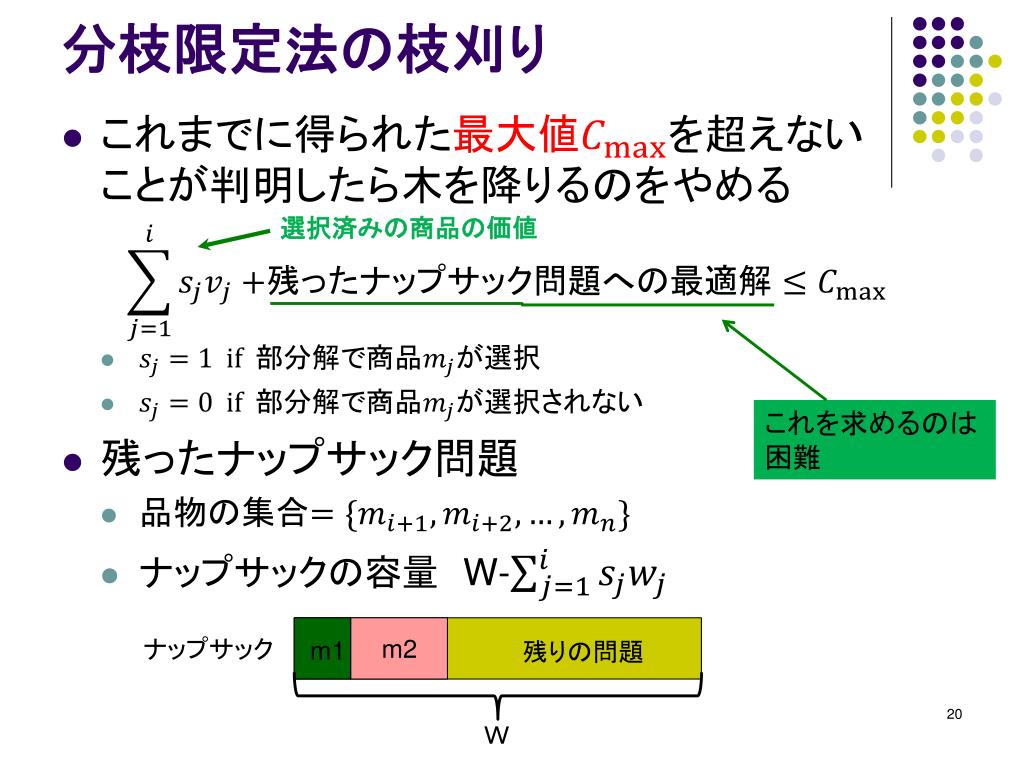
01ナップサック問題を分枝限定法で解く 私は現在JavaScriptを用いて01ナップサック問題を分枝限定法で解くプログラムを書いています。 流れとしては荷物の個数をもとに列挙木を作り、暫定解をもとに最適でない解が見つかれば再起を用いて1つ前の葉に戻ればよいのではないかと考えておりますがうまく実装ができません。 そこで質問なのですが、上限値及び、下記分枝限定法の適用 (0) 近似最適解を暫定解とする。 暫定解:x=(1, 0, 1, 0)T 暫定値:z*=8 (1) x 1=0 に固定した部分問題を解く (a)より部分問題の最適解x=(0,1, 1, 0)Tが得ら れたから終端できる 目的関数値z=9 は暫定値z*=8より大きいから、これ *分枝限定法 分枝カット法 動的計画法 ... 近似解法最適解を求めることを諦めて,ある程度最適値に近い値をもつ実 行可能解をなるべく早く求める 制度保証付き近似解法 メタヒューリスティック(タブーサーチ,遺伝的アルゴリズ ム,アニーリング法



Atcoder Abc32 D ナップザック問題を分岐限定法で爆速で解く Qiita


連載コラム 数理最適化 第5回 数理最適化とその歴史 貴社ビジネスのit共創者 中央コンピューター株式会社
・分枝限定法:組合せ最適化問題の最適解を求める主要な方法 ・欲張り法:準最適解を求めることができる。最適解が 得られる保証はない。 ・吝嗇法:欲張り法の逆の考え方。最適解が得られる保証はない。分枝限定法の手順(9)部分問題が全て終端し、チェックすべき部分問題が無い ・原問題から派生した部分問題が全て終端した。 ・従って、このときの暫定解( )0,1,1,0 7と暫定解 が最適解である。資料1 分枝限定法基礎 第7回: 分枝限定法(2) (スライド) 分枝限定法に基づくナップサック問題の解法 クイズ6 解答 資料1 ナップザック問題の定式化 第8回: ゲーム木における探索法(1) (スライド)



Ppt 最適化ワークショップ 整数計画法の発展と応用 整数計画法チュートリアル モデリングと解法 Powerpoint Presentation Id


組合せ最適化問題と厳密解法 最小木 ナップサック問題 ビンパッキング 巡回セールスマン問題 Lpによる上界 下界 分枝限定法 Ppt Download
概要 01ナップサック問題を分枝限定法の結果が一致しない。 私は今01ナップサック問題を解こうとしています。 しかし、出力結果が私の思い描いていたものとは違っておりどうすればよいのかわかりません。 データとしては 容量が10のナップサックで入れたいものはそれぞれ、 番号0 W = 4 V = 32 番号1 W = 7 V = 35 番号2 W = 6 V = 24ナップサック問題 を 分枝限定法 (Branch and Bound) で解きます。 分枝限定法(ぶんしげんていほう、英 branch and bound, BB)は、 各種最適化問題(特に離散最適化と組合せ最適化)の最適解を求める汎用アルゴリズムである。 分枝操作と限定操作から構成される。 全ての解候補を体系的に列挙するもので、最適化された量の上限と下限の概算を使って、最適でない候補はナップサック問題を分枝限定法で解く アイテム ガム あめ りんご パフ とろり チョコ 山盛り 煎餅 いも チップラムネ しっとり クッキー 値段aj (十円) 5 1 13 15 8 7 21 価値cj 2 1 8 7 4 6 3 8 効率cj/aj 040 100 062 035 027 075 043 038 貪欲アルゴリズムを使って求めた解


Y S R ら ぶ ぱ ぴ 完 走 し ま し た アルペで分かる 整数計画法5 伊400 だが手がないわけではない Ip問題に有効な手段の一つとして 分枝限定法がある 伊402 困難は分割せよ 分枝 限定操作によって 最適解の範囲を順次狭めていくこと


分枝 Japaneseclass Jp
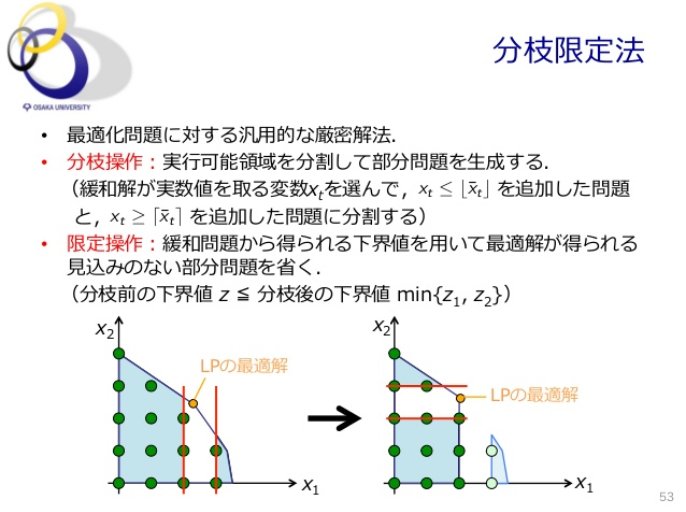
分枝操作: ∈0,1のいくつかを固定 緩和:連続化 ∈0,1により解の上界を与える –連続緩和した問題は簡単(𝑞 / が大きい方から詰める) 分枝限定法の別の例: ナップサック問題;n) ナップサック問題の解は変数の整数条件を外した 線形最適化問題の解とは一般には一致しない 欲張り法も最適解が得られる保証はない分枝限定法(ぶんしげんていほう、英 branch and bound, BB )は、各種最適化問題(特に離散最適化と組合せ最適化)の最適解を求める汎用アルゴリズムである。 分枝操作(英 branching operation )と限定操作(英 bounding operation )から構成される。 全ての解候補を体系的に列挙するもので、最適化さ



Approximation Algorithms For Combinatorial Optimization Problems Speaker Deck



Ppt 情報システム基盤学 基礎 1 アルゴリズムとデータ構造 Powerpoint Presentation Id
分枝限定法 •なぜこんなことが起きるのか? → IP を解くアルゴリズムの理解が必須 •分枝限定法 (branch & bound method) IP を場合分け(分枝)しながら, 各ノードで対応した IP の連続緩和問題 (IP から整数条件を除いた問題)を解き, その緩和問題の最適値が図1 01 ナップサック問題に対する分枝木 31 分枝限定法 分枝限定法は,一部の変数を固定しつつそれぞ れの場合を調べ上げていくという考え方に基づい ている.この過程は,図1 のような図(分枝木と 呼ぶ)を用いて表現できる.一番上の点1は元の分枝限定法の考え方 • 問題を場合分けによって部分問題に分解(分枝操作) • 01ナップサック問題: 各変数について0 の場合と1 の場合に分ける • 分枝の進行の様子は探索木により表現可能 • これだけでは,解の全列挙と同じ,時間がかかる


7 3 分枝限定法の並列化の利用


第2回 ナップサック問題を色々な方法で解いてみた ブレインパッドの数理最適化ブログ Platinum Data Blog By Brainpad
・分枝限定法:組合せ最適化問題の最適解を求める主要な方法 ・欲張り法:準最適解を求めることができる。最適解が 得られる保証はない。 ・吝嗇法:欲張り法の逆の考え方。最適解が得られる保証はない。次のナップサック問題を分枝限定法により解け。 (問題 KP0 )max 15x 118x 26x 32x 4 subject to 4 1 x5x 22x 3x 4 ≦ 6 1, xx 2, x 3, x 4 ∈{0,1} ただし、子問題選択は以下の規則に従うこと。 (1) 奥行優先則 (2) 幅優先則 演習課題 62 次のナップサック問題を動的計画ナップザック問題(分枝限定法) 目的 ナップザック問題とは、 「$n$個の荷物がありそれぞれ($i=1,2,,n$)に価値$v_i$と重さ$w_i$が設定されています。 遠足には合計の重さが$W$以下の荷物しか持っていけません。


4 4 離散形最適化のアルゴリズム ものづくり のためのjmaオンラインセミナー 日本能率協会



組合せ最適化問題と厳密解法 最小木 ナップサック問題 ビンパッキング 巡回セールスマン問題 Lpによる上界 下界 分枝限定法 Ppt Download
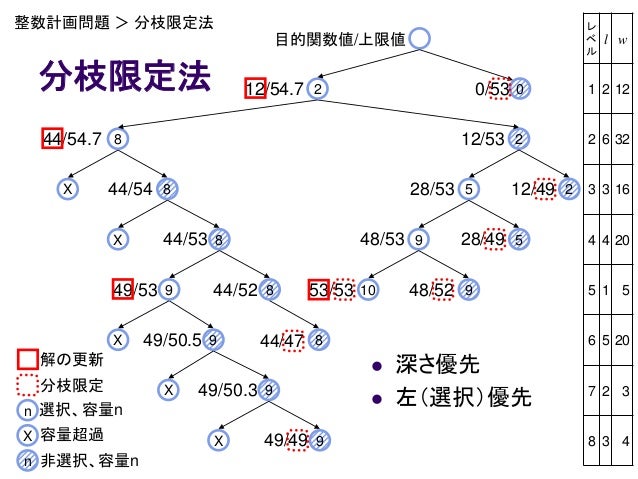
分枝限定法(ぶんしげんていほう、英 branch and bound, BB )は、各種最適化問題(特に離散最適化と組合せ最適化)の最適解を求める汎用アルゴリズムである。 分枝操作(英 branching operation )と限定操作(英 bounding operation )から構成される。 全ての解候補を体系的に列挙するもので、最適化さ例ナップサック問題に対する分枝限定法 ナップサックの容量W max = 112 要素 重さ 6 25 30 40 30 60 10 腕づく 方 全数探索 合 検 す 解候補数 重さ 価値 15 100 90 60 40 15 10 3 ・腕づくの方法(全数探索)の場合、検討する解候補数は28=256次のナップサック問題を分枝限定法により解け。 (問題 KP0 )max 15x 118x 26x 32x 4 subject to 4 1 x5x 22x 3x 4 ≦ 6 1, xx 2, x 3, x 4 ∈{0,1} ただし、子問題選択は以下の規則に従うこと。 (1) 奥行優先則 (2) 幅優先則 演習課題 62 次のナップサック問題を動的計画



Pdf File



組合せ最適化
動的計画法(ナップサック問題) 動的計画法とナップサック問題について解説します。 動的計画法とは 直接計算すると大きな時間がかかってしまう問題に対し、途中の計算結果をうまく再利用することで計算効率を上げる手法のこと。切除平面法,分枝限定法 分枝カット法 解きやすさ (理論的) (実際的) easy (P) hard (NP) 大規模問題も解ける 解ける問題規模が拡大中 1947年 単体法(Dantzig) 1957~60年 分枝限定法(MarkowitzManne, Eastman, LandDoig) 切除平面法(Gomory) 「はじめよう」 の理由



Mathematical Optimization In 60 Minutes Speaker Deck



第2回 ナップサック問題を色々な方法で解いてみた ブレインパッドの数理最適化ブログ Platinum Data Blog By Brainpad



ページサンプル閲覧 達人出版会



大きなナップサック 解説 おじい研究所



第2回 ナップサック問題を色々な方法で解いてみた ブレインパッドの数理最適化ブログ Platinum Data Blog By Brainpad


Operations Research Yonezawa No2



Mathematical Optimization In 60 Minutes Speaker Deck



B 2 3 分枝限定法



Efficient Algorithms For Combinatorial Optimization Problems Speaker Deck



情報工学概論 アルゴリズムとデータ構造 09動的計画法01ナップサック問題01問題設定と用語 Youtube


ナップサック問題に対する分枝限定法 Youtube



ソフトウェアii 第4回 12 10 ソフトウェアii



1995 号 最適解探索方式および最適解探索方法 Astamuse



情報工学概論 アルゴリズムとデータ構造 09動的計画法01ナップサック問題01問題設定と用語 Youtube


1 welcome 情報数理研究室 理工学3号館1階北側中央部分 Ppt Download


組合せ最適化問題と厳密解法 最小木 ナップサック問題 ビンパッキング 巡回セールスマン問題 Lpによる上界 下界 分枝限定法 Ppt Download


資材切出し問題と列生成法



0 1 ナップザック問題について 2 T Nakaの阿房ブログ


図で見る分枝限定法 Qiita



大きなナップサック 解説 おじい研究所



分枝限定法 ヤマカサの競技プログラミング



知能情報処理 第1回 この授業の概要 組合せ最適化問題とは Ppt Video Online Download



04 号 問題分割方法 最適化方法 問題分割装置 最適化装置 及びコンピュータプログラム Astamuse



組合せ最適化



1995 号 最適解探索方式および最適解探索方法 Astamuse


Ppt 情報システム基盤学 基礎 1 アルゴリズムとデータ構造 Powerpoint Presentation Id



組合せ最適化



0 1 ナップザック問題について 2 T Nakaの阿房ブログ



Operations Research Yonezawa No2



図で見る分枝限定法 Qiita
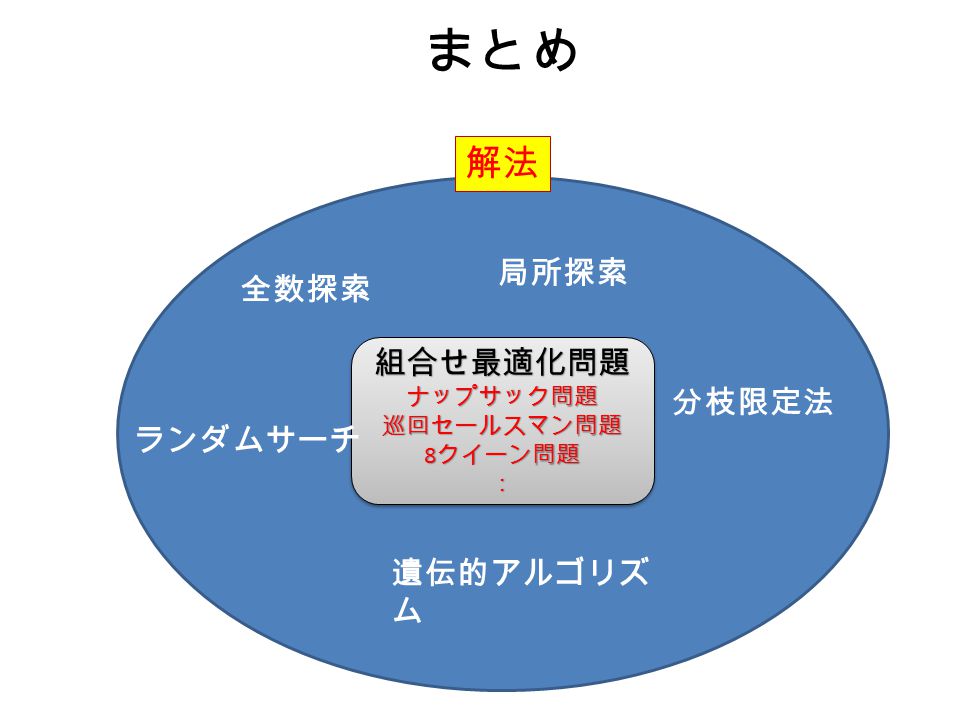


知能情報処理 第1回 この授業の概要 組合せ最適化問題とは Ppt Video Online Download



知能情報処理 第1回 この授業の概要 組合せ最適化問題とは Ppt Video Online Download



1995 号 最適解探索方式および最適解探索方法 Astamuse
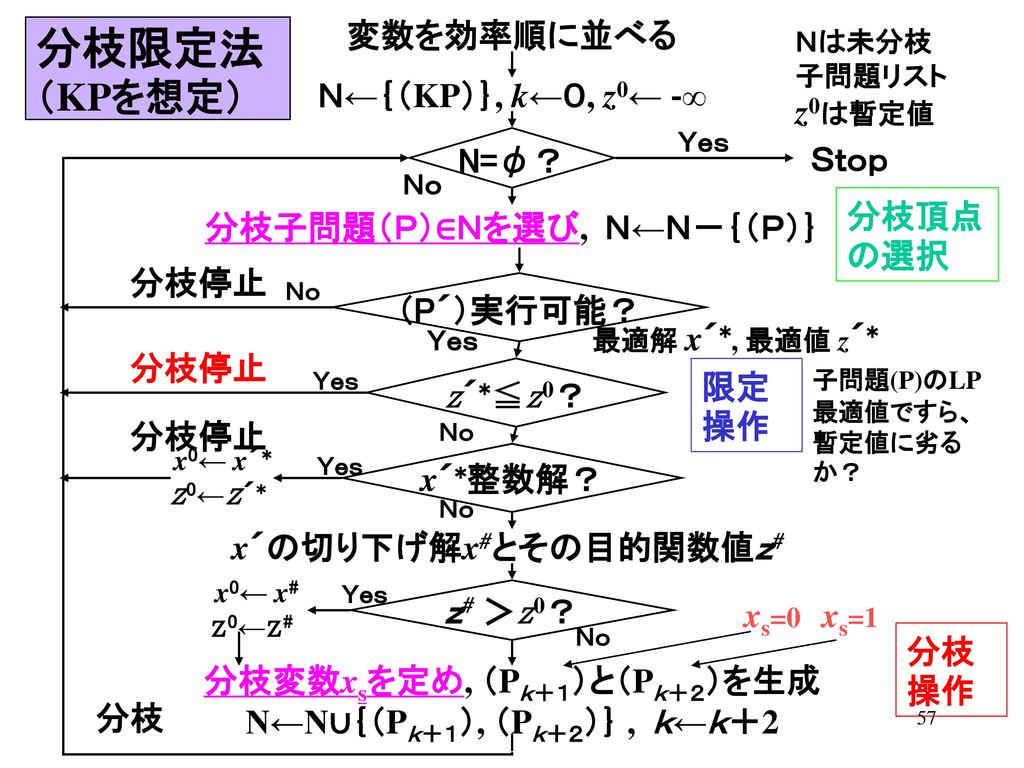


基礎or or演習 第6回 11 17 09 森戸担当分中間試験 来週 11 24 火 13 00は試験 Ppt Download



Atcoder Abc32 D ナップザック問題を分岐限定法で爆速で解く Qiita



組合せ最適化問題と厳密解法 最小木 ナップサック問題 ビンパッキング 巡回セールスマン問題 Lpによる上界 下界 分枝限定法 Ppt Download



ナップサック問題に対する分枝限定法 Youtube



B 2 3 分枝限定法



組合せ最適化



混合整数線形計画法 Mip アルゴリズム 入門



ナップサック問題の分枝限定法 Likeな最適化操作をjumpを使って動作確認する
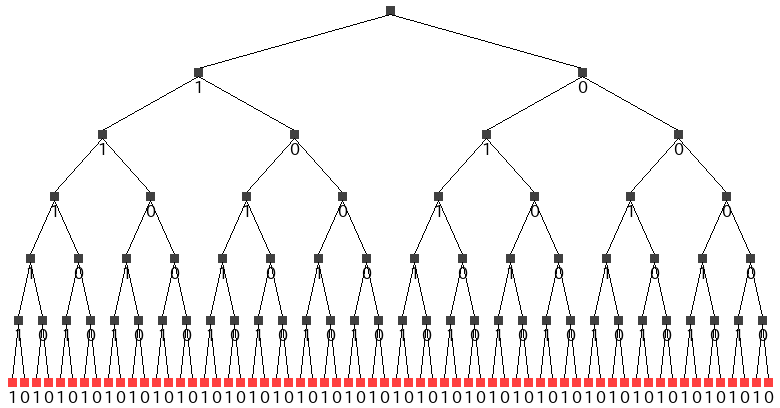


図で見る分枝限定法 Qiita



組合せ最適化入門 線形計画から整数計画まで


大きなナップサック 解説 おじい研究所



組合せ最適化問題と厳密解法 最小木 ナップサック問題 ビンパッキング 巡回セールスマン問題 Lpによる上界 下界 分枝限定法 Ppt Download



動的計画法 ナップサック問題 アルゴリズム講習会


連載コラム 数理最適化 第5回 数理最適化とその歴史 貴社ビジネスのit共創者 中央コンピューター株式会社



組合せ最適化
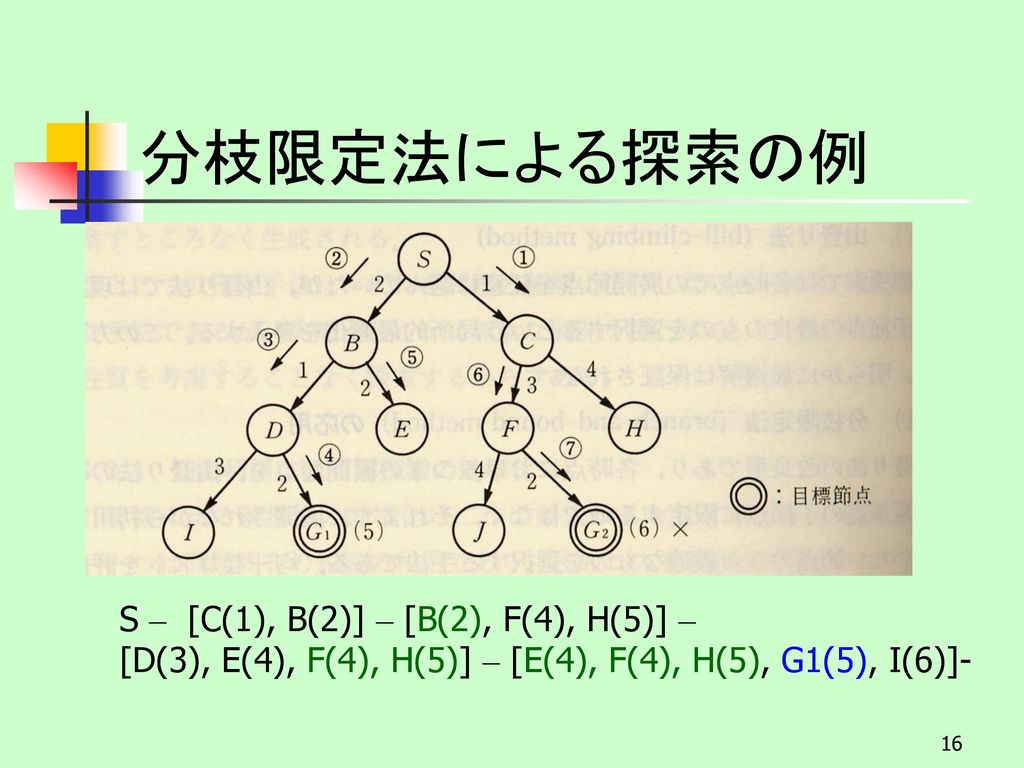


第8回 問題解決 Ppt Download
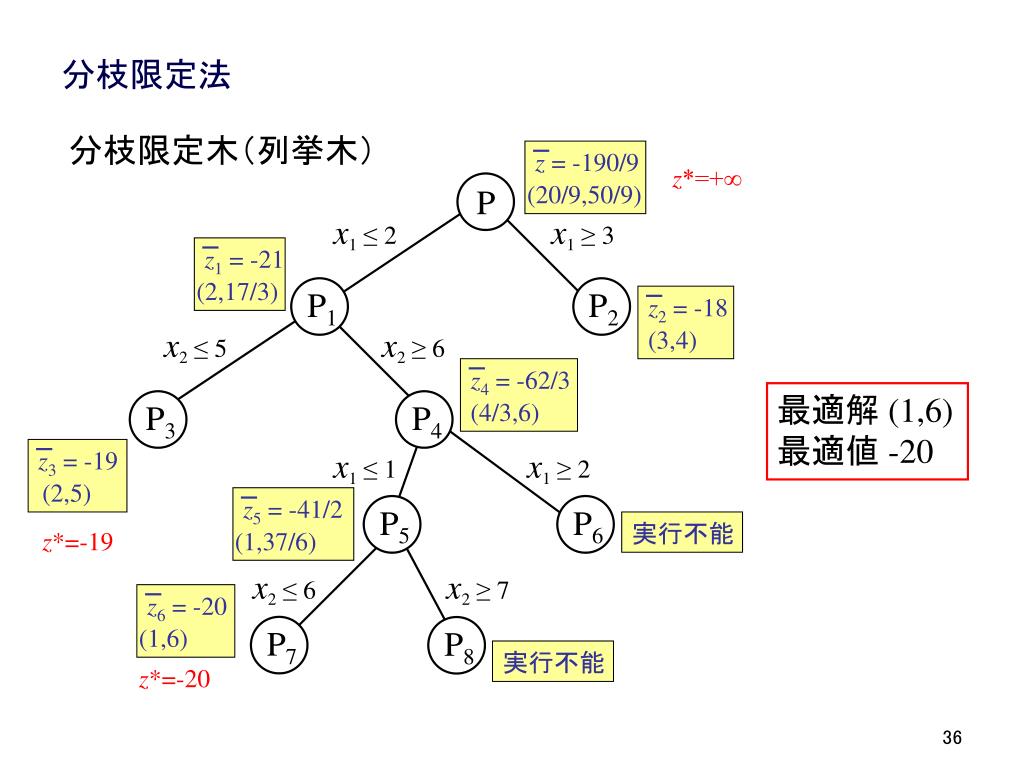


Ppt 最適化ワークショップ 整数計画法の発展と応用 整数計画法チュートリアル モデリングと解法 Powerpoint Presentation Id
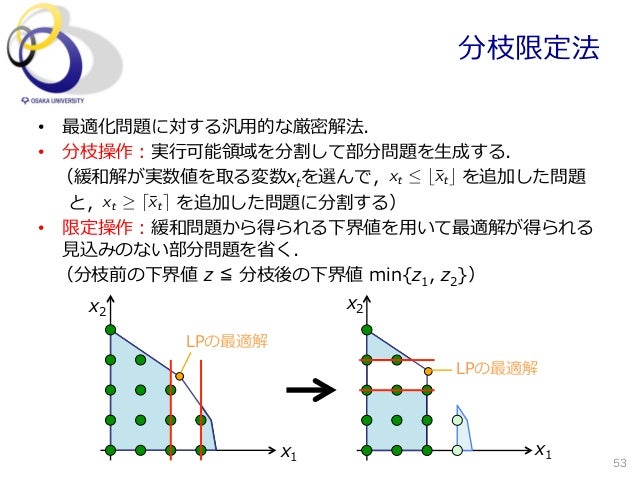


組合せ最適化入門 線形計画から整数計画まで



0 件のコメント:
コメントを投稿